Python: How to Solve Basic Mathematical Problems (Part I)

We will learn how to solve basic mathematical problems in Python.

Computing Factorials using Python

Computing the factorial of a number generally means to multiply and keep on multiplying the given number with a number 1 less than the previous number until it reaches zero. They are denoted by the “!” symbol. This algorithm can also be denoted by a single mathematical expression.

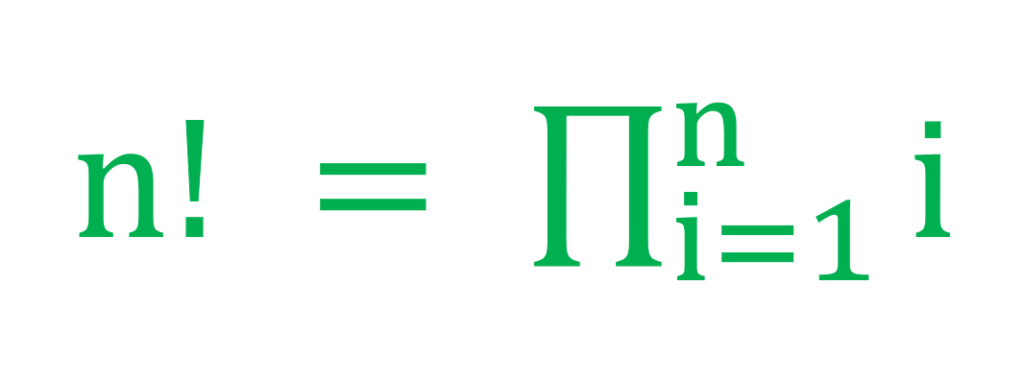
Now, the factorial can be calculated in two different ways. They are –

1. using a loop ( for/while )
2. using recursion

Computing Factorial using a loop :

In this method, any loop can be used. I shall be approaching this method using for loop.

General Idea:-

1. The loops can start from either 1 or n
2. We also need to declare a variable (say F) of type int & initialize by 1
3. If we start from n, then the loop needs to traverse from n to 1. Thus the iterator needs to decrease by 1
4. Similarly, if we are starting from 1, then the iterator needs to increase by 1
5. For every change in the iterator, multiply the iterator with F.
6. At the end of the loop, the factorial of n will be stored in the variable F

Let’s implement this with the help of a python code:–

num = int(input("Enter a number : "))
F = 1
for i in range(num):
    F = F*num
    num-=1
print("Factorial is = ",F)

You should try to implement this approach with a while loop instead of for loop

Computing Factorial using recursion:

A recurring function is one that calls itself many times while it is being executed. This approach can simplify many complex problems; one such being how to calculate the factorial of a number.

If you pay close attention you may observe that n! = n × n-1 × n-2 … × 2 × 1

We can then rewrite the formula as — n! = n × (n-1)!

This exact same idea is used to find factorial via recursion. Note that once we pass n as the argument into the function, the function would return the product of n & (n-1)! . But to calculate (n-1)! the function needs to call itself again, which in turn will again call itself. If uncontrolled, this may cause a memory error. Thus whenever the “n-1” is equal to 1, we should instruct the program to stop. This can be done by returning a constant value instead of a function call. Thus the final value will be the product of all numbers from n to 1.

General Idea:-

1. Accept an integer argument n into the function
2. If n is greater than 1, then return the product of n & (n-1)!
3. If n is less than or equal to 1, then return a constant value instead of a function call
4. The constant value is always 1 because 1! = 0! =1
5. In the end, we will get the products of all numbers from n to 1
6. Note that 0! does make sense, hence we should ensure that condition is given as n<=1 & not just n=1

Let’s implement this with the help of a python code:–

def factorial(n):
    if n<=1:
        return 1
    else:
        return n*factorial(n-1)

num = int(input("Enter the number : ")) 
print("Factorial is = ",factorial(num))

The Fibonacci Sequence using Python

The Fibonacci sequence is one of the many famous sequences in the world & was discovered by the Italian mathematician Leonardo Fibonacci.

About the sequence – The sequence starts from the digit 1 & then the next digit in the series is the sum of the previous two digits. Therefore the sequence is as follows: 1, 1, 2, 3, 5, 8, 13, 21 …

When we talk about a Fibonacci sequence, we generally try to find the nth Fibonacci term or find n terms of a Fibonacci. We shall try to tackle both these problems.

Similar to the previous problem, this can also be approached in two ways

1. using Loop
2. using Recursion

Finding n^th Fibonacci term :-

Let us assume the 1st term = 1, 2nd term = 1 & so on.

Thus according to the formula, n^th Fibonacci term = (n-1)Fibonacci term + (n-2)Fibonacci term. This problem looks familiar. Observe that at the end, we need to call a function that will compute the (n-1)^th Fibonacci term which in turn calls the same function to compute the (n-3)^th Fibonacci term. Therefore we can solve this with the help of recursion.

General idea –

1. The function shall accept a single integer argument.
2. If the value of the argument is less than or equal to 2, then the function should return a constant value.
3. The constant value is 1 here because the 1st & 2nd Sequence in Fibonacci is 1
4. If the parameter is greater than 2, then the function should return the sum of the last two terms in the Fibonacci sequence

Let’s see the actual python code

def Fib(n):
    if n<=2:
        return 1
    else:
        return Fib(n-1) + Fib(n-2)
        
num = int(input("Enter the number : "))
print(num,"th Fibonacci term is ",Fib(num))

Note that this can also be approached by using a loop. Here instead of moving from the nth term to the 1st, instead, we need to move from the 1st to the nth term. We take a variable as storage & keep adding the previous two sums to generate the nth Fibonacci term. Let’s see the actual code for this particular approach

term = int(input("Enter term for Fibonacci sequence: "))
num1,num2,temp=1,1,0
for i in range(1,term-1):
    temp=num1+num2 
    num1=num2 
    num2=temp
print(term,"th Fibonacci term is ",temp)

Generating n terms of the Fibonacci Sequence:-

Observe that in the range of for loop, we are taking up to term-1 because once it enters a for loop, the value of temp changes. Hence we need to adjust the range of for loop.

In previous problems, we were generating the nth Fibonacci sequence. There we did generate the individual terms, but it was overwritten with the preceding/succeeding terms. Here, our approach will be similar to the previous problem & whenever we obtain a new term, we should quickly print it.

The actual python code –

term = int(input("How many terms to generate of the Fibonacci Sequence  : "))
num1,num2,temp=1,1,0
print("Terms are : 1,1,",end="")
for i in range(1,term-1):
    temp=num1+num2 
    num1=num2 
    num2=temp
    print(temp,end=",")

Note that we have used the loop method because the recursion method doesn’t generate the individual terms technically.

This article thus covered two basic mathematical problems with the help of python. In the next post, we shall discuss some more interesting mathematical problems & try to solve them with python.

Spread the word!