Python: Working with a special set of numbers

Today we will learn how to work with a special set of numbers in Python. We will see the pseudocode along with the real Python code.

Summation of Series using Python

Computing the sum of n numbers present in a set is very straightforward. The approach is explained by the following pseudocode.

1) Declare a variable (say SUM ) & assign it a value of zero
2) Initiate a for loop starting from the first element in the set/array & ending at the last element
3) Add the current element to the variable SUM
4) The loop moves forward till it reaches the last element
5) Exit the for loop & print the value of variable SUM

Code

Here is the corresponding Python code

Set = [5,2,6,7,8,9,1,4,6,0,7,2]
SUM=0
for element in Set:
    SUM = SUM + element
print("The set of element were : ",Set)
print("Their sum is : ",SUM)

You can also modify the code so that one has to perform n-1 addition for adding n numbers. This can be achieved by declaring the initial value of the variable SUM equal to the value of the first element of the Set. Then start the for loop from i=1 up to i=length of Set. The modified code is written below.

Set = [5,2,6,7,8,9,1,4,6,0,7]
SUM=Set[0]
for i in range(1,len(Set)):
    SUM = SUM + Set[i]
print("The set of element were : ",Set)
print("Their sum is : ",SUM)

Before moving further one should learn how to create an array of random sizes (say from 1 to 100) & filled it with random integers from 0 to 100. This would save a lot of time. This can be easily done by making use of the random module. Let’s see the corresponding code.

#creating an array of random size filled with random values.

import random

size_UL=25                 #upper limit for the size of the array
size_LL=1                  #lower limit for the size of the array
val_UL=100                 #upper limit for the random values in array
val_LL=0                   #lower limit for the random values in array
Arr=[None]*random.randint(size_LL,size_UL)      #creating an array of random size
for i in range(0,len(Arr)):
    Arr[i]=random.randint(val_LL,val_UL)        #Inserting random values in the array

print("Your random array is : \n",Arr)

Now that we have learned to create a random array & to take the sum of all elements in the array, let us see what all problems can be solved with it.

Generating Averages using Python

The algorithm for this is :

1. Get an array either from user input or by generating it randomly
2. Remember that average = ( ∑ element ) ÷ ( no. of elements )
3. Pass the array into the sum method. It will calculate the sum as discussed earlier.
4. Return the computed sum to the method which will get the average.
5. Compute the average from the above-mentioned formula; here it’s the sum/length of the array

Code

Here is the code for getting average

def generate_array(sLL,sUL,vLL,vUL):
    import random                 
    Arr=[None]*random.randint(sLL,sUL)      
    for i in range(0,len(Arr)):
        Arr[i]=random.randint(vLL,vUL)        
    return Arr

def find_sum(Set):
    SUM=Set[0]
    for i in range(1,len(Set)):
        SUM+=Set[i]
    return SUM

def get_average(array):
    sum_value = find_sum(array)
    return sum_value / len(array)

List=generate_array(1,20,0,101)
print("The numbers are :\n",List)
print("\nThe average is :\n",get_average(List))

We first create a random array using the method & store it in the variable “List”. Then call the get_average() method which takes the random array as the input. After calling, the get_average() method calls another method find_sum() which computes the sum of the numbers present in the array. Then it calculates the average by dividing the sum by the length of the array. After that, the value is printed. Try to execute the code yourself.

Generating Harmonic Means

The harmonic mean for a set of n numbers is given by the formula :

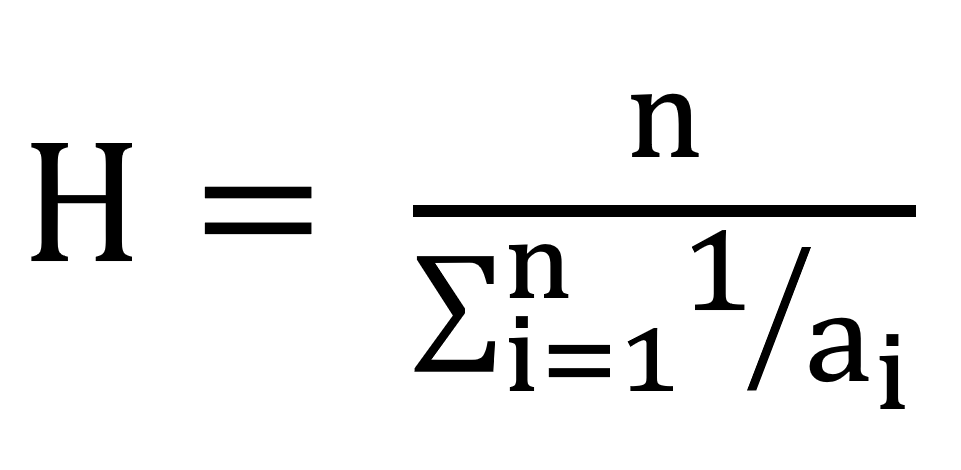
This problem also involves the summation of numbers in a series but with a slight twist in the formula. Let’s see the code for this problem. Instead of calculating the sum of individual elements, we need to calculate the sum of the inverse of the individual elements. Thus the new code is as follows:

import arrays

List=arrays.generate(1,20,0,101)
Sum=0
for element in List:
    Sum = Sum + (1/element)
HMean = len(List) / Sum

print(List)
print("Harmonic Mean is : ",HMean)

In the above code, we have called the generate() function which resides in the arrays module. The code for this has already been mentioned in this post earlier.

Now, let us see some special cases for a set of numbers. Here we will try to find the sum but in a quicker manner.

Some Special Cases

1. L = 1, 2, 3, … ,n
2. L = 1, 3, 5, … ,n
3. L = 2, 4, 6, … ,n
4. L = 1, 2, 4, 8, 16, 32, … ,n

These are simple mathematical problems. We need to first identify the category in which the input sequence should lie. Then determine the number of elements. At last, plug the numbers into the mathematical formula to obtain the sum. Let’s discuss a few mathematical formulas which can help simplify these problems.

• Sum of N natural numbers = 0.5 * N(N+1)
• Sum of N odd numbers = N*N = N²
• Sum of N even numbers = N(N+1)
• Sum of first N powers of 2 = 2ⁿ⁺¹ – 1

Let’s see the code for how to compute the sum for special sets of numbers.

Code

#summation for special set of numbers
#Basically advanced version for find_sum() method

while True:
    L = input("Enter your special set of numbers separated only by , (commas) \n>>> ")
    L = L.split(",")
    is_natural,is_odd,is_power2,is_even,is_spcl = False,False,False,False,False
    Sum=0
    
    for i in range(0,len(L)):
        
        if L[i].isnumeric():
            L[i] = int(L[i])
        
    for i in range(1,len(L)):

        if (L[0]==0 or L[0]==1):        
        
            if L[i-1]+1 == L[i]:
                is_natural=True
            else:
                is_natural=False
                
            if L[i-1]+2 == L[i]:
                is_odd=True
            else:
                is_odd=False

            if L[i] == L[i-1]*2:
                is_power2=True
            else:
                is_power2=False

        elif L[0]==2:
            
            if L[i-1]+2 == L[i]:
                is_even=True
            else:
                is_even=False

        else:
            is_spcl=False

    if (True) not in [is_natural,is_even,is_odd,is_power2]:
        is_spcl=False

    N = len(L)
    if is_spcl:
        

        if is_natural:
            Sum=0.5*N*(N+1)
        elif is_odd:
            Sum=N*N
        elif is_power2:
            Sum=(2**(N))-1
        elif is_even:
            Sum=N*(N+1)
        else:
            print("Not a special sequence")

    else:
        
        Sum=L[0]
        for i in range(1,N):
            Sum+=L[i]
    print("\nThe sequence of numbers are :\n>>> ",L)
    print("\nAnd its Sum is ",Sum)
    ch=input("Press x to exit & any other key to continue :\t")
    if ch.lower()=="x":
        break
    print("\n")

In the above code, we have to check if the given sequence belongs to the four special cases or not. If they belong to a special case then we calculate the Sum directly by the mathematical formula. Otherwise, the sum is computed manually using them for a loop. The overall algorithm used in the code has been discussed below.

• Accept numbers using the separator. Then split it & allocate them to a List
• Declare the necessary variables & set the criteria that the sequence belongs to a special case as False
• Check whether they belong to a special case & then accordingly classify them
• If they don’t belong to a special sequence, then mention this
• Calculate the sum according to the mathematical formula
• Print the sequence & its sum
• Ask the user if they want to try again or else quit the program.

Try to solve these

• L = 1/1 + 1/2 + 1/3 + … + 1/n
• L = 1-1+1-1+1 … n (for even as well as odd number of terms)
• L = 2-4+6-8 … n
• L = -1+3-5+7 … n

Hope this post gave a clear insight regarding the summation of a set of numbers & also for special cases. Some more special cases have also been attached. You may try to solve them using the logic discussed earlier & also with the help of some mathematical formulae.